Sensor specifications
| MPY-01 | MPY-RS | MPY-RS2 | SPY | |
|---|---|---|---|---|
| Responsivity (kV/W)* | 7.5 | 13 | 70 | 7.5 |
| Noise (µV/√Hz) | 13 | 18 | 25 | 13 |
| NEP (pW/√Hz)* | 1500 | 1400 | 400 | 1500 |
| Detectivity (cm√Hz/W)* @ 10 Hz | 1.8⋅108 |
2.0⋅108 |
5.0⋅108 | 1.8⋅108 |
| Detectivity (cm√Hz/W)* @ 1 kHz | 0.4⋅108 | 1.1⋅108 | 2.0⋅108 | 0.4⋅108 |
|
Wavelength range (depends on window) |
UV to Far-IR | UV to Far-IR | UV to Far-IR | UV to Far-IR |
| Bandwidth (-3 dB) | 200 Hz | 3 kHz | 8 kHz | 200 Hz |
| Frequency range (-20 dB) | 1 Hz - 1 kHz | 1 Hz - 20 kHz | 1 Hz - 50 kHz | 1 Hz - 1 kHz |
| Power supply |
MN21 battery (>30h operating time) |
Low noise power supply (±12V, Thorlabs LDS12B) |
Low noise power supply (±12V, Thorlabs LDS12B) |
Low noise power supply (±12V, Thorlabs LDS12B) |
| Dimensions (mm) |
h: 76.0 w: 48.5 d: 22.9 |
h: 71.5 w: 45.3 d: 25.5 |
h: 71.5 w: 45.3 d: 25.5 |
h: 24.3 w: 28.0 d: 12.9 |
| Datasheet | MPY-01 | MPY-RS | MPY-RS2 | SPY |
* Measured with broadband black body source at 150°C, central wavelength λ = 6.8 µm and KBr window
Available detector windows
| Material | Transmission region | ||
|---|---|---|---|
| Wavelength | Frequency | Wavenumber | |
| KBr | 200 nm - 30 µm | (10 - 1,500) THz | (333 - 50,000) cm-1 |
| CsI | 400 nm - 40 µm | (7.5 - 750) THz | (250 - 25,000) cm-1 |
| Si | > 1.2 µm | < 250 THz | < 8,333 cm-1 |
| PTFE | (20 - 40) µm and > 60 µm | (7.5 - 15) THz and < 5 THz | (250 - 500) cm-1 and < 167 cm-1 |
| HDPE | > 40 µm | < 7.5 THz | < 250 cm-1 |
| Diamond |
> 225 nm |
< 1,332 THz |
< 44,444 cm-1 |
Not sure which detector is best for you?
Please ask yourself these 6 questions:
- What repetition rate is your light source?
Pyroelectric detectors can only observe a change of radiation intensity - continuous wave (CW) sources will not give a signal. If you want to measure a CW source, you have to chop the beam at a frequency suitable for your detector. The MPY-RS and MPY-RS2 detectors can be used for repetition rates / chopping frequencies of many kHz.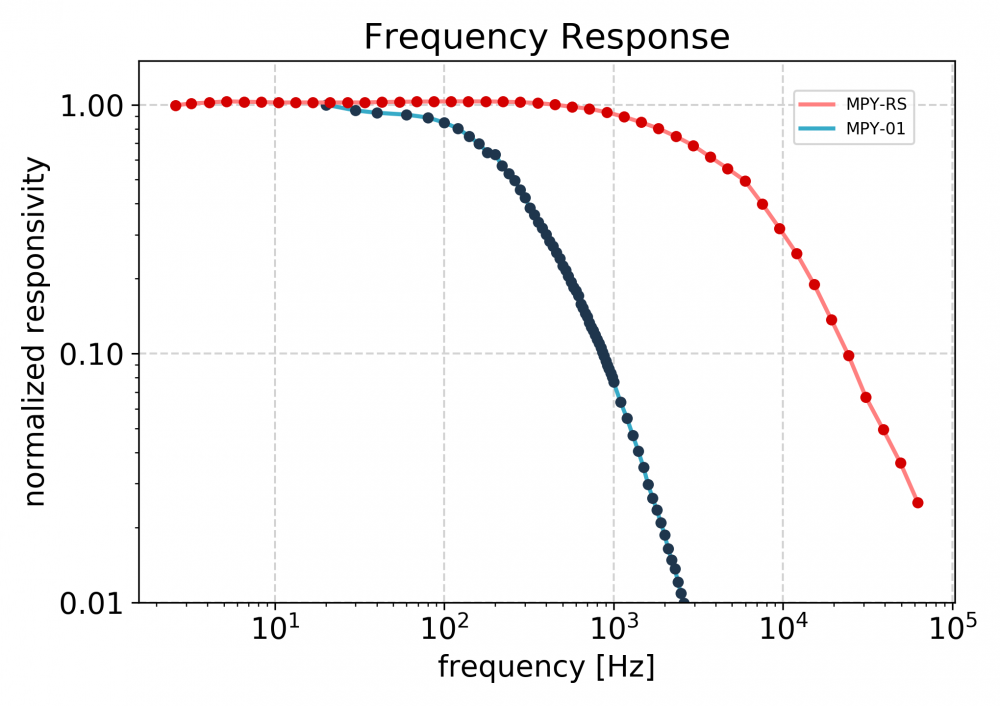
- What is your expected incident power range?
All detectors are highly sensitive. If you want to measure higher power you probably need to attenuate your beam (see our tutorial). If you want to measure very low signal levels, the MPY-RS2 is our most sensitive detector model. - Do you need an external power supply for long-term measurements?
The MPY-RS, MPY-RS2 and SPY detectors are powered by an external power supply. - Do you need vacuum compatibility?
Take a look at our SPY vacuum compatible version. - Do you have size limitations in your setup?
Compare the detector dimensions (see table 1 above). The SPY detector has the smallest footprint. - Which incident wavelength range do you want to cover?
Our pyroelectric detectors are sensitive from the UV to the terahertz / far infrared. The usable wavelength range only depends on the detector window. We offer various windows for all detectors (see table 2 above).
